Calculating The Perimeter Of Formula: Your Complete Guide To Measuring Shapes
Have you ever looked at a garden bed you want to build, or maybe a room you plan to redecorate, and wondered how much fencing or trim you'd actually need? It's a pretty common thought, you know, and the answer often comes down to something called perimeter. Figuring out the distance around things, that's what we're talking about here, and it's a skill that, as a matter of fact, comes in handy more often than you might think.
This idea of perimeter, it's actually just the total length of a shape's boundary, or the distance around its outside edge. It's determined by adding up the length of all the sides and edges enclosing the shape, which, you know, sounds simple enough. From designing architectural plans to working on landscaping projects, understanding the perimeter of formula is really quite essential for making sure things fit and look just right.
So, we're going to explore what perimeter means, why it's so useful, and how to calculate it for all sorts of shapes. We'll look at the specific perimeter of formula for common figures, and you'll see how, in a way, this basic geometric concept helps us in our daily lives. By the end, you'll feel much more comfortable with these calculations, I mean, honestly, it's pretty straightforward once you get the hang of it.
Table of Contents
- What Exactly is Perimeter?
- Why Does the Perimeter of Formula Matter?
- Common Perimeter Formulas for Everyday Shapes
- Square
- Rectangle
- Triangle
- Circle (Circumference)
- Parallelogram
- Trapezoid
- Ellipse
- Regular Octagon
- Sector of a Circle
- Real-World Applications of the Perimeter of Formula
- Your Go-To Perimeter Calculator
- Frequently Asked Questions About Perimeter
- Getting Started with Perimeter Calculations
What Exactly is Perimeter?
Perimeter, to put it simply, refers to the total distance around the sides of a polygon or any other geometric shape. It's the measurement of the boundary, or the outline, of a closed figure. Think of it like walking along the edge of a field; the total distance you walk is the perimeter of that field. This idea, you know, is really quite fundamental in geometry.
In geometry, the perimeter of a shape is defined as the total length of its boundary. It's determined by adding the length of all the sides and edges enclosing the shape. So, if you have a shape with several straight sides, you literally just add up the measurements of each side. It's a very direct way to find out how much "around" something there is.
For shapes with curved boundaries, like a circle, the process is a little different, but the core idea remains the same: finding the total distance along the edge. The units we use for perimeter are typically linear measurements, such as millimeters (mm), centimeters (cm), meters, kilometers (km), inches, feet, or yards. This means, as a matter of fact, that perimeter is always a single dimension, a length.
Why Does the Perimeter of Formula Matter?
Understanding the perimeter of formula is, well, pretty important for a lot of practical reasons. It's not just some abstract math concept you learn in school and then forget. This calculation is, for example, an essential part of designing architectural plans. Imagine an architect needing to figure out how much baseboard trim is needed for a room; that's a perimeter calculation right there.
Landscaping projects also rely heavily on perimeter. If you're planning a new flower bed, you might need to know its perimeter to buy the right amount of edging material. Or, say you're building a fence around your yard, you'd definitely need to know the perimeter to purchase the correct length of fencing. It's all about figuring out the "around" measurement, which, you know, is pretty crucial for material estimates.
Creating various items, too, often involves perimeter. A dressmaker might need to know the perimeter of a neckline to cut the right amount of bias tape. Even something like a rectangular package sent by a delivery service can have a maximum combined length and girth (which is the perimeter of a cross-section) of 120 inches, as described in my text. So, you see, it's actually a very practical measurement that helps us plan and build things accurately.
Common Perimeter Formulas for Everyday Shapes
Now, let's get down to the specifics of the perimeter of formula for various common shapes. My text mentions that you'll find perimeter formulas for twelve different shapes, and that's really helpful. While a perimeter calculator can make things super easy, knowing the formulas yourself is, you know, pretty empowering.
Square
A square is a four-sided shape where all sides are equal in length, and all angles are right angles. So, to find its perimeter, you just need to know the length of one side. If we call the side length 's', then the perimeter of formula for a square is simply: Perimeter = 4 × s. For instance, if a square has a side of 10 inches, its perimeter would be 40 inches. This is, you know, pretty straightforward.
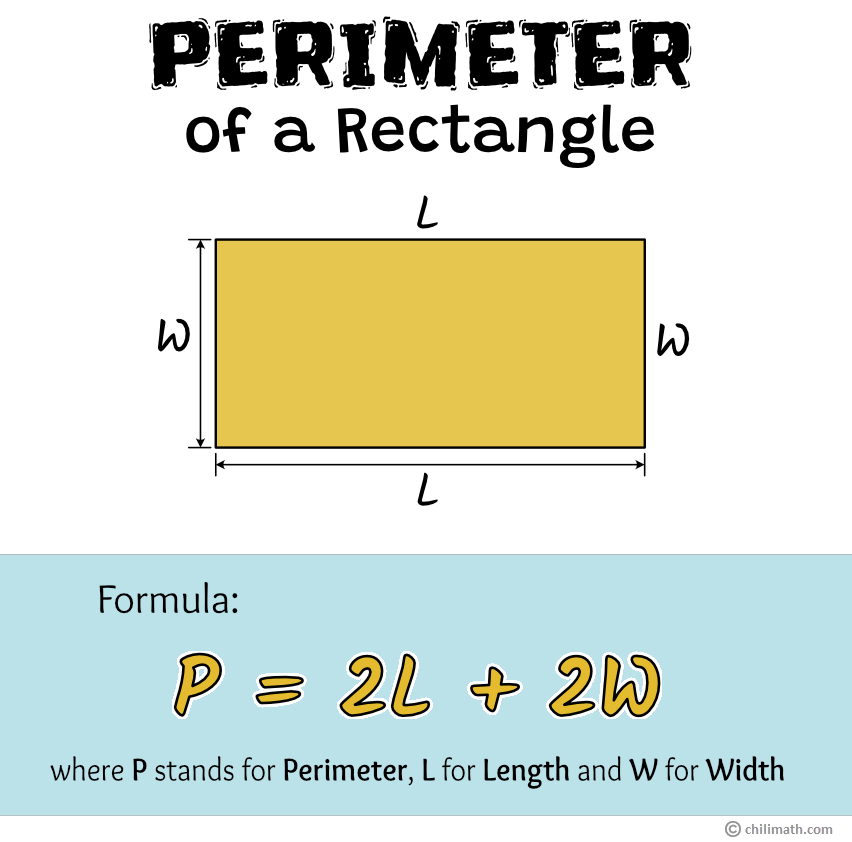
Rectangle
A rectangle also has four sides, but opposite sides are equal in length, and all angles are right angles. It has a length ('l') and a width ('w'). To find the perimeter, you add up two lengths and two widths. The perimeter of formula for a rectangle is: Perimeter = 2 × (l + w). So, if a rectangle is 12 cm long and 5 cm wide, its perimeter would be 2 × (12 + 5) = 2 × 17 = 34 cm. This is, in a way, just adding up all the sides.
Triangle
A triangle is a three-sided polygon. The perimeter of formula for any triangle is simply the sum of the lengths of its three sides. If the sides are 'a', 'b', and 'c', then: Perimeter = a + b + c. It doesn't matter if it's an equilateral, isosceles, or scalene triangle; you just add the lengths of its unique sides. This is, basically, the most fundamental perimeter calculation there is.
Circle (Circumference)
For a circle, the perimeter has a special name: circumference. It's the distance around the circular boundary. The circumference depends on the circle's radius ('r') or its diameter ('d'). The perimeter of formula for a circle uses the mathematical constant Pi (approximately 3.14159). So, Circumference = 2 × Pi × r, or Circumference = Pi × d. For example, a circle with a radius of 7 meters would have a circumference of 2 × Pi × 7, which is about 43.98 meters. It's a little different, you know, because of the curve.
Parallelogram
A parallelogram is a four-sided shape where opposite sides are parallel and equal in length. It has two different side lengths, often called 'a' and 'b'. The perimeter of formula is similar to a rectangle's, because it also has two pairs of equal sides: Perimeter = 2 × (a + b). If a parallelogram has sides of 8 feet and 5 feet, its perimeter would be 2 × (8 + 5) = 2 × 13 = 26 feet. So, it's pretty easy to calculate, really.
Trapezoid
A trapezoid is a four-sided shape with at least one pair of parallel sides. The other two sides can be of different lengths. To find the perimeter of a trapezoid, you simply add the lengths of all four of its sides. If the sides are 'a', 'b', 'c', and 'd', then: Perimeter = a + b + c + d. There isn't a shortcut formula like for rectangles or squares, you know, because the sides can all be different.
Ellipse
An ellipse is like a stretched circle, an oval shape. Calculating the exact perimeter of formula for an ellipse is actually quite complex and involves advanced mathematics, often using an infinite series or approximations. For most practical purposes, a common approximation is: Perimeter ≈ Pi × [1.5 × (a + b) - sqrt(a × b)], where 'a' and 'b' are the lengths of the semi-major and semi-minor axes. It's not as simple as a circle, that's for sure, but there are calculators that can help with this.
Regular Octagon
A regular octagon is an eight-sided polygon where all sides are equal in length and all interior angles are equal. Similar to a square, if you know the length of one side ('s'), you can find the perimeter by multiplying that length by the number of sides. The perimeter of formula for a regular octagon is: Perimeter = 8 × s. This is, you know, very similar to how you find the perimeter of any regular polygon.
Sector of a Circle
A sector of a circle is a portion of a circle enclosed by two radii and an arc. To find its perimeter, you need to add the lengths of the two radii and the length of the arc. The arc length ('L') is found using a portion of the circle's circumference, typically L = (angle/360) × 2 × Pi × r, where 'angle' is the central angle in degrees. So, the perimeter of formula for a sector is: Perimeter = r + r + L, or Perimeter = 2r + L. It's a bit more involved than a full circle, but still manageable, you know, once you have the arc length.
Real-World Applications of the Perimeter of Formula
The perimeter of formula pops up in so many real-world situations, it's almost surprising how often we use it without thinking. We've talked about architectural plans and landscaping, but there are even more examples. For instance, if you're a keen crafter, you might need to calculate the perimeter of a piece of fabric to add a decorative border. That's a practical use, you know.
Consider sports fields, too. The track around a running field is essentially a large perimeter. Knowing its length is crucial for athletes training for races. Or, think about fencing a property. My text mentions wanting "perimeter in your community" which, while perhaps referring to security boundaries, still connects to the idea of defining and measuring outer limits. Understanding these outer limits, you know, is really quite vital.
Even in more complex scenarios, like the problem described in my text about a Norman window (a semicircle atop a rectangle) or a pentagon formed by a triangle on a rectangle, finding the maximum area given a fixed perimeter involves using these formulas. These are optimization problems, and they show just how versatile the perimeter of formula can be in engineering and design. It's pretty cool, actually, how a simple concept can lead to complex solutions.
Your Go-To Perimeter Calculator
While knowing the perimeter of formula for each shape is very helpful, sometimes you just need a quick answer, especially for more complex shapes like an ellipse or a sector of a circle. My text points out that "With this perimeter calculator, you don't need to worry about perimeter calculations anymore." This is, you know, a pretty big relief for many people.
A good perimeter calculator can easily figure out the perimeter of common bodies like a square, rectangle, triangle, circle, parallelogram, trapezoid, ellipse, regular octagon, and sector of a circle. You just input the measurements, and it does the math for you. These tools often work with both imperial and metric units, so whether you're dealing with millimeters, centimeters, meters, kilometers, inches, feet, or yards, it can handle it. You can learn more about geometric measurements on our site, which might help too.
Using a calculator is particularly handy when you're working on a project and need quick, accurate results without having to remember every single formula or double-check your arithmetic. It's a very practical tool that complements your understanding of the formulas. So, while you're getting better at understanding the perimeter of formula, a calculator can be your reliable helper, you know, for those times when speed is key.
Frequently Asked Questions About Perimeter
What is the basic formula for perimeter?
The most basic perimeter of formula is simply adding up the lengths of all the sides of a polygon. For example, for a triangle with sides a, b, and c, the perimeter is a + b + c. This principle, you know, applies to any shape with straight sides; you just sum them up.
How do you find the perimeter of a rectangle?
To find the perimeter of a rectangle, you use the formula: Perimeter = 2 × (length + width). You add the length and the width together, and then you multiply that sum by two. This is because a rectangle has two equal lengths and two equal widths. It's a pretty handy formula, honestly.
Why is perimeter important?
Perimeter is important because it helps us measure the boundary or outline of shapes, which is essential for many real-world applications. It's used for estimating materials like fencing, trim, or borders in architectural plans and landscaping projects. It helps us, you know, figure out how much "stuff" we need to go around something.
Getting Started with Perimeter Calculations
Understanding the perimeter of formula really helps you in so many practical ways, from home projects to more complex design work. It's a fundamental concept that, you know, just keeps showing up. Whether you're measuring a square garden plot or trying to figure out the circumference of a circular pool, the principles are the same: you're finding the total distance around the edge.
Practice is key here. Try measuring things around your home, like the perimeter of a tabletop or a picture frame. Use the formulas we've discussed, and then maybe check your work with an online calculator. The more you work with these concepts, the more natural they'll feel. You might find that you're using these skills more often than you ever thought possible, which is, you know, pretty cool.
Remember, the goal is to make these calculations easy and accessible for you. There are many resources available to help you along the way. You can always refer back to this guide, or even explore more about various geometric shapes to deepen your knowledge. Just keep practicing, and you'll be a perimeter pro in no time, I mean, it's just about getting comfortable with the numbers.

4 Ways to Find the Perimeter of a Rectangle - wikiHow
Perimeter of Rectangle - Definition, Formula & Examples | ChiliMath

Difference Between Area and Perimeter - Basics, Definitions, Examples.